Содержание
1. Введение
Тригонометрия — раздел математики, изучающий соотношения между углами и сторонами треугольников и других геометрических фигур. Название происходит от греческих слов "trigon" (треугольник) и "metron" (измерение), что буквально означает "измерение треугольников".
Актуальность исследования
В современном мире тригонометрия играет фундаментальную роль в развитии науки и технологий. От расчета орбит космических аппаратов до создания медицинских томографов — тригонометрические функции являются математической основой множества практических применений.
- Астрономические вычисления и навигация
- Геодезические измерения и картография
- Медицинская диагностика и визуализация
- Биологические исследования и моделирование

Единичная окружность и основные тригонометрические функции
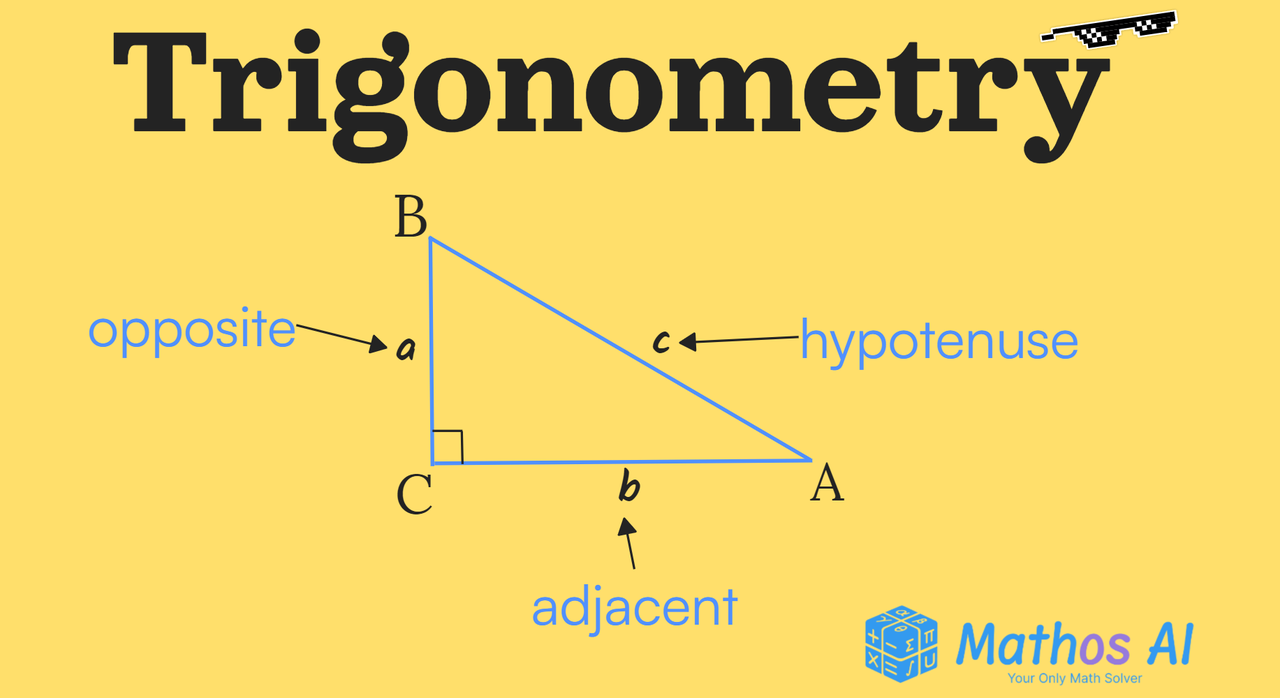
Графики основных тригонометрических функций
Основные тригонометрические функции
Синус
$\sin \alpha = \frac{противолежащий}{гипотенуза}$
Косинус
$\cos \alpha = \frac{прилежащий}{гипотенуза}$
Тангенс
$\tan \alpha = \frac{\sin \alpha}{\cos \alpha}$
2. Историческая справка
История тригонометрии охватывает более двух тысячелетий развития математической мысли. Тригонометрию создали древние астрономы для решения практических задач измерения небесных расстояний и навигации.
Древний Египет и Вавилон (2000-1000 до н.э.)
Первые применения соотношений в прямоугольных треугольниках. Папирус Ринда содержит задачи на определение наклона пирамид.
Древняя Греция (III-II века до н.э.)
Аристарх Самосский использует тригонометрические соотношения для вычисления расстояний до Солнца и Луны. Гиппарх создает первые таблицы хорд.
Птолемей (II век н.э.)
"Альмагест" содержит обширные пятизначные таблицы хорд и теорему Птолемея для вычисления тригонометрических функций.
Индия (V-XII века)
Введение синуса и косинуса как самостоятельных функций. Разработка формул для синуса половинного угла и синуса суммы углов.
Арабский мир (VIII-XIII века)
Аль-Хорезми, аль-Баттани и другие математики развивают сферическую тригонометрию для астрономических вычислений.
Европа (XIV-XVI века)
Региомонтан вводит тангенс, составляет точные таблицы. Коперник применяет тригонометрию в гелиоцентрической системе мира.
Ключевые этапы развития
Древность
Практические задачи астрономии и землемерия
Средневековье
Систематизация и табулирование функций
Новое время
Аналитическая тригонометрия и комплексные числа
Современность
Цифровые технологии и компьютерные вычисления
3. Теоретические основы
Тригонометрические функции представляют собой периодические функции, описывающие соотношения между углами и сторонами в геометрических фигурах.
Основные тригонометрические тождества
Основное тригонометрическое тождество:
$\sin^2 \alpha + \cos^2 \alpha = 1$
Формулы приведения:
$\sin(\pi/2 - \alpha) = \cos \alpha$
Формулы сложения:
$\sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$
Формулы двойного угла:
$\sin 2\alpha = 2\sin \alpha \cos \alpha$
Теорема синусов
$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R$
где R — радиус описанной окружности
Теорема косинусов
$c^2 = a^2 + b^2 - 2ab\cos C$
обобщение теоремы Пифагора
Свойства тригонометрических функций
| Функция | Период | Область значений | Четность |
|---|---|---|---|
| $\sin x$ | $2\pi$ | $[-1, 1]$ | Нечетная |
| $\cos x$ | $2\pi$ | $[-1, 1]$ | Четная |
| $\tan x$ | $\pi$ | $(-\infty, +\infty)$ | Нечетная |
4. Применение в астрономии
Астрономия была первой наукой, которая потребовала развития тригонометрии. Измерение расстояний до небесных тел, определение их положения и движения — все это основано на тригонометрических вычислениях.
Метод параллакса
Самый важный метод измерения расстояний до звезд основан на тригонометрии. Параллакс — это угловое смещение звезды при наблюдении с разных точек орбиты Земли.
$d = \frac{1}{p}$ парсек
где p — параллакс в угловых секундах
Триангуляция
Метод определения расстояний и координат небесных объектов путем измерения углов в треугольниках, образованных наблюдательными пунктами и объектом.
$d = \frac{b \sin C}{\sin A}$
где b — базис, A и C — измеренные углы
Исторический пример: Аристарх Самосский
В III веке до н.э. Аристарх попытался определить расстояние до Солнца, используя тригонометрию. Он рассматривал прямоугольный треугольник Земля-Луна-Солнце во время квадратуры Луны.
$\frac{d_{Солнце}}{d_{Луна}} = \frac{1}{\cos 87°} \approx 19$
Реальное отношение ≈ 400 (ошибка из-за неточности измерений)
Современные применения
Космическая навигация
Расчет траекторий космических аппаратов
Радиоастрономия
Определение положения радиоисточников
Спутниковая геодезия
GPS и ГЛОНАСС системы
5. Применение в геодезии
Геодезия — наука об измерении Земли — неразрывно связана с тригонометрией. От определения формы и размеров Земли до создания точных карт — все основано на тригонометрических вычислениях.

Метод тригонометрического нивелирования

Теодолит — основной инструмент геодезиста
Тригонометрическое нивелирование
Определение превышения точек местности по измеренным углам наклона и расстояниям:
$h = D \cdot \tan \alpha + i - v$
где D — горизонтальное расстояние, α — угол наклона, i — высота инструмента, v — высота визирования
Основные задачи геодезии
Прямая геодезическая задача
По известным координатам точки, дирекционному углу и расстоянию найти координаты второй точки:
$x_2 = x_1 + d \cos \alpha$
$y_2 = y_1 + d \sin \alpha$
Обратная геодезическая задача
По координатам двух точек найти расстояние и дирекционный угол между ними:
$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$
$\tan \alpha = \frac{y_2-y_1}{x_2-x_1}$
Измерение Земли: от Эратосфена до современности
Эратосфен (276-194 до н.э.)
Первое определение размеров Земли по длине тени в разных городах:
$R = \frac{L \cdot 360°}{7.2° \cdot 2\pi} \approx 6300$ км
Современные методы
Спутниковая геодезия и лазерная дальнометрия обеспечивают точность до миллиметров в глобальном масштабе.
Современные применения
Картография
Создание точных карт и планов
Строительство
Разбивка зданий и сооружений
Навигация
GPS/ГЛОНАСС системы
Геология
Поиск полезных ископаемых
6. Применение в медицине
Современная медицина широко использует тригонометрию в диагностических технологиях, анализе биологических ритмов и медицинском оборудовании.
МРТ и КТ — современные методы диагностики
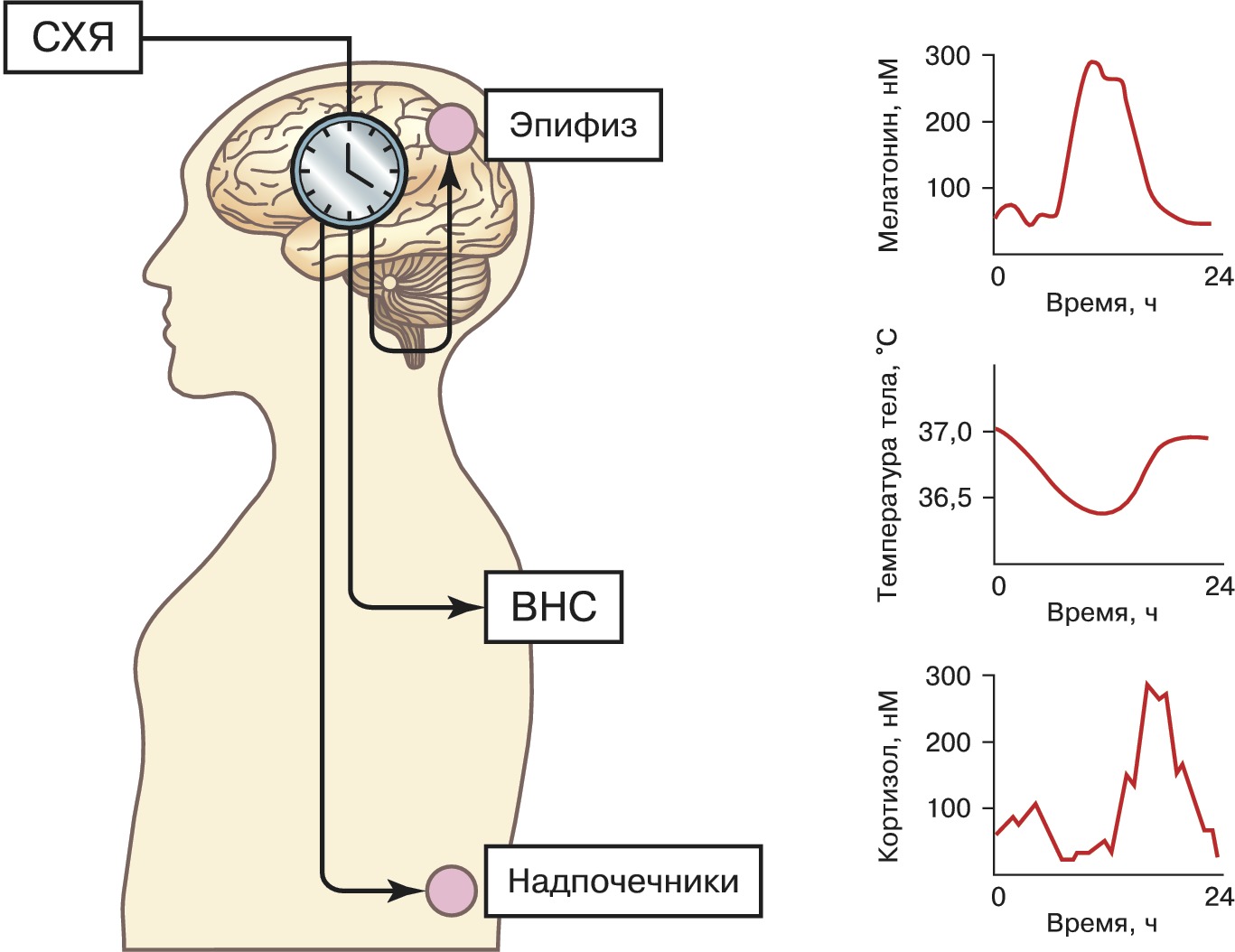
Циркадные ритмы человека
Компьютерная томография (КТ)
КТ использует математический метод, основанный на преобразовании Радона и обратном преобразовании Фурье, которые тесно связаны с тригонометрическими функциями.
$f(x,y) = \int_0^{2\pi} \int_{-\infty}^{\infty} P(\rho, \theta) \cdot e^{2\pi i \rho (x\cos\theta + y\sin\theta)} d\rho d\theta$
Обратное преобразование Радона для реконструкции изображения
Биоритмы и тригонометрия
Многие биологические процессы имеют циклический характер и могут быть описаны синусоидальными функциями.
Физический ритм
Период: 23 дня
$y = \sin\left(\frac{2\pi t}{23}\right)$
Эмоциональный ритм
Период: 28 дней
$y = \sin\left(\frac{2\pi t}{28}\right)$
Интеллектуальный ритм
Период: 33 дня
$y = \sin\left(\frac{2\pi t}{33}\right)$
Электрокардиография (ЭКГ)
Анализ сердечного ритма часто использует разложение в ряд Фурье для выделения различных компонент сигнала.
$f(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} [a_n \cos(n\omega t) + b_n \sin(n\omega t)]$
Разложение ЭКГ-сигнала в ряд Фурье
Медицинские синусы
В анатомии термин "синус" используется для обозначения полостей и каналов:
Синусовый узел сердца
Естественный водитель ритма, генерирующий электрические импульсы
Каротидный синус
Барорецепторная зона для регуляции кровяного давления
Венозные синусы
Специализированные венозные коллекторы в черепе
Параназальные синусы
Воздухоносные полости в костях черепа
7. Применение в биологии
Биология изобилует периодическими процессами — от колебаний популяций до биоритмов организмов. Тригонометрические функции позволяют математически описывать эти природные циклы.

Суточные биоритмы человека
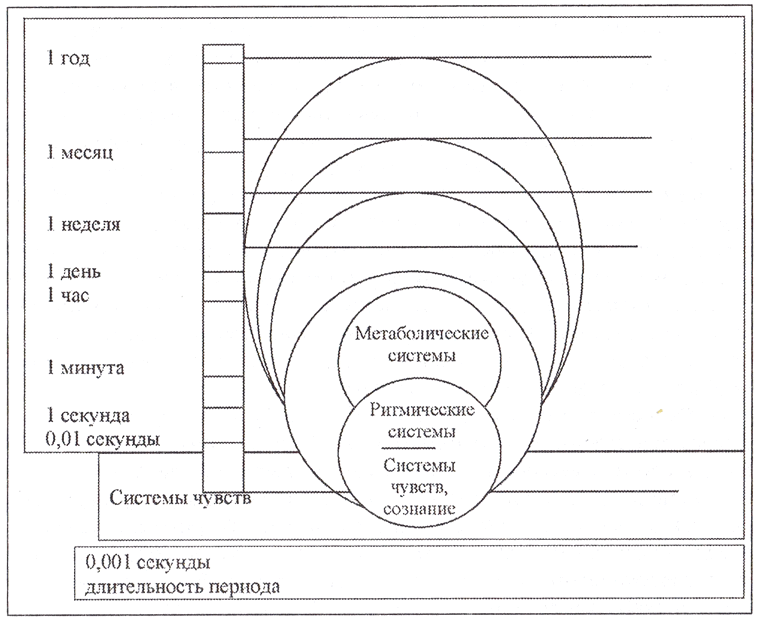
Электрофизиологические ритмы мозга
Циркадные ритмы
Суточные биологические ритмы регулируют множество физиологических процессов и могут быть описаны синусоидальными функциями.
$A(t) = A_0 + A_1 \cos\left(\frac{2\pi t}{T} + \phi\right)$
где T = 24 часа (циркадный период), φ — фазовый сдвиг
Движение рыб и тригонометрия
Волнообразное движение рыб и других водных животных описывается синусоидальными функциями.
Математическая модель
Форма тела плывущей рыбы в момент времени t:
$y(x,t) = A(x) \sin\left(\frac{2\pi}{\lambda}x - \omega t + \phi\right)$
где A(x) — амплитуда, зависящая от положения вдоль тела
Типы плавания
- Ангуиллиформное: волна проходит по всему телу (угорь)
- Каранксиформное: волна только в задней части (тунец)
- Остракиформное: движение только хвостовым плавником
Популяционная динамика
Колебания численности популяций в экосистемах часто описываются системами уравнений с тригонометрическими решениями.
Модель "хищник-жертва" (Лотка-Вольтерра)
Система уравнений:
$\frac{dx}{dt} = ax - bxy$
$\frac{dy}{dt} = cxy - dy$
Периодическое решение:
Численности популяций колеблются по закону, близкому к синусоидальному
Биологические осцилляторы
Сердечный ритм
Периодические сокращения сердца
Частота: 1-2 Гц
Дыхательный ритм
Циклические дыхательные движения
Частота: 0.2-0.3 Гц
Мозговые ритмы
Электрические колебания мозга
Частота: 0.5-100 Гц
Биохимические осцилляции
Многие биохимические процессы имеют колебательный характер, например, концентрация гормонов в крови.
Пример: Колебания концентрации кортизола
Концентрация гормона стресса кортизола в крови изменяется по циркадному ритму:
$C(t) = C_0 + A \cos\left(\frac{2\pi t}{24} + \phi\right)$
Максимум утром, минимум вечером
8. Заключение
Проведенное исследование показало, что тригонометрия является фундаментальной основой для понимания и описания множества явлений в различных областях науки и техники.
Основные выводы исследования
Универсальность применения
Тригонометрические функции находят применение во всех изученных областях — от измерения космических расстояний до описания биологических ритмов.
Историческая преемственность
Методы, разработанные древними астрономами, продолжают использоваться в современных высокотехнологичных применениях.
Междисциплинарность
Тригонометрия служит связующим звеном между различными науками, обеспечивая единый математический язык описания.
Практическая значимость
Без тригонометрии невозможно функционирование современных технологий — от GPS до медицинской томографии.
Значение для каждой области
Астрономия
Тригонометрия остается основой для определения расстояний во Вселенной, навигации космических аппаратов и изучения структуры космоса.
Геодезия
Современные методы картографии, строительства и навигации базируются на тригонометрических принципах, заложенных тысячелетия назад.
Медицина
Медицинская диагностика XXI века — КТ, МРТ, анализ биоритмов — невозможна без математического аппарата тригонометрии.
Биология
Понимание жизненных процессов — от движения живых организмов до колебаний популяций — требует тригонометрического описания.
Перспективы развития
Новые технологии
- • Квантовые вычисления
- • Искусственный интеллект
- • Робототехника
- • Биоинженерия
Исследовательские направления
- • Космическая геодезия
- • Телемедицина
- • Экологическое моделирование
- • Нейроинформатика
Заключительная мысль
"Тригонометрия — это не просто раздел математики, а универсальный язык, на котором природа описывает свои циклические процессы и геометрические закономерности. От древних астрономов до современных ученых — человечество использует этот мощный инструмент для понимания и освоения окружающего мира."
Источники и литература
1. История тригонометрии — Википедия: https://ru.wikipedia.org/wiki/История_тригонометрии
2. Применения тригонометрии в астрономии, географии, геодезии — NSPortal: https://nsportal.ru
3. Тригонометрия в медицине и биологии — Инфоурок: https://infourok.ru
4. Метод тригонометрического нивелирования — НВК Горгеомех: https://gorgeomeh.ru
5. Биологические ритмы — Большая российская энциклопедия: https://old.bigenc.ru